2021-05-13

SWAG(Sliding Window Aggregation)再考

本記事は1年半ほど前に執筆した
motsu-xe.hatenablog.com
という記事の続編ではあるのですが、暇な人以外はそっちは読まないでもいいです。

(忙しい人はしばらく下まで読み飛ばしてください)
こんにちは、Motsu_xeです。ありがたいことに、前作の記事はGoogle検索の影響もあり、未だにちょくちょくアクセスされているのですが、話題になってたから調べてみて、よくわかんなかったのがわかった！と思ったタイミングで、自分の浅い理解に基づいて書かれた記事となっておりますので、流石にこれを皆様にそのままご提供し続けるのもどうかと思い*1、筆をとった次第です。

本記事は、前回の浅い理解から、相対的に深くなった理解で、SWAGを今の私の理解に基づいて、解説していきたいと考えています。正直前の記事は消したい気持ちすらありますが、ありがたいことにあれを読んでSWAG理解できた、みたいな声を何人か聞いておりますので、まああれも人によっては刺さるかなということで残してはおきます。

前提知識

stack
queue
半群の定義*2
償却計算量の概念*3

SWAGとは

前回の記事では、SWAGを半群の列に対して、連続する要素の総積を尺取り的に求めるデータ構造として紹介しましたが、今回は少し変えます。

Sliding Window Aggregationとは、以下の4つの操作を、時間計算量償却 $\Theta(1)$ で実行するデータ構造である。

$\mathrm{new}()$ 半群の元を要素とする空のqueueを生成する

$\mathrm{push}(x)$ queueに $x$ を追加する

$\mathrm{pop}()$ queueの先頭の要素を削除する

$\mathrm{fold}()$ queueに入っている要素の総積*4を計算する

$\mathrm{new}()$	半群の元を要素とする空のqueueを生成する
$\mathrm{push}(x)$	queueに $x$ を追加する
$\mathrm{pop}()$	queueの先頭の要素を削除する
$\mathrm{fold}()$	queueに入っている要素の総積*4を計算する

少し考えると、前回のデータ構造と本質的に同じであることがわかると思います。

SWAGのstack版

SWAGは少し難しいので、少し変更してstackで同じことを考えます。STAGとでも呼びましょうか。つまり

STAGとは、以下の4つの操作を、時間計算量償却 $\Theta(1)$ *5で実行するデータ構造である。

$\mathrm{new}()$ 半群の元を要素とする空のstackを生成する

$\mathrm{push}(x)$ stackに $x$ を追加する

$\mathrm{pop}()$ stackの末尾の要素を削除する

$\mathrm{fold}()$ stackに入っている要素の総積を計算する

$\mathrm{new}()$	半群の元を要素とする空のstackを生成する
$\mathrm{push}(x)$	stackに $x$ を追加する
$\mathrm{pop}()$	stackの末尾の要素を削除する
$\mathrm{fold}()$	stackに入っている要素の総積を計算する

を考えます。これは簡単で、stack内の要素の累積積を保持しておけば、簡単に実行できます。擬似コードで書くと以下のようになりす。

new():
    st = stack()

push(x):
    if st.empty():
        st.push(x)
    else:
        st.push(top(st) * x)

pop():
    pop(st)

fold():
    return st.top()

two-stack queue

一旦SWAGのことは忘れて、queueについて考えます。queueはstack2本で再現することができます。詳しい話は他の記事に譲ることにして、擬似コードで書くと

new():
    stf = stack()
    stb = stack()

push(x):
    stb.push(x)

move():
    if stf.empty():
        while not stb.empty():
            stf.push(stb.top())
            stb.pop()

pop():
    move()
    stf.pop()

front():
    move()
    return stf.top()

のようになります。stfからstbに要素を移すタイミングで要素数だけ時間がかかりますが、各要素は、pushされてからpopされるまでに、高々1回しか移動しないことを考えれば、償却 $O(1)$ となっていることがわかります。

stack上のデータ構造をqueueに載せる

上で述べたstack版のSWAGを2つ用意すると、two-stack queueを用いることで、SWAGを実装することができます。これは、queue全体に対するfoldが、2つのstackのそれぞれのfoldの結合により求められることからわかります。ただし、非可換の場合は若干注意が必要で、2つのstackに乗っている半群は、演算を左右反転させたものとなっていて、stbには半群 $S$ 、stfには $S^{\mathrm{op}}$ が載っているという感じになっています。*6また、moveするときに、back側の累積を取る前の生データが必要になることに注意すると、次の擬似コードのように実装できます。

new():
    stf = STAG<S^op>()
    stb = STAG<S>()
    stb_row = stack()

push(x):
    stb.push(x)
    stb_row.push(x)

move():
    if stf.empty():
        while not stb.empty():
            stb.pop()
            stf.push(stb_row.top())
            stb_row.pop()

pop():
    move()
    stf.pop()

fold():
    if stf.empty():
        return stb.fold()
    if stb.empty():
        return stf.fold()
    return stf.fold() * stb.fold() //stf.fold()の値もSの元と解釈する

これでSWAGの本質は説明終了です。実際に実装するときは、わざわざSTAGのようなものは作らず、そのまま書いた方がわかりやすいです。*7

応用

queueと同様、dequeも2つのstackにより再現できることが知られています。詳しくは他の記事に譲りますが、two-stack queueとほぼ同様で、popしようとしたときに、popしたいstackが空だったら、半々に分けるみたいな感じでできます。STAGをSWAGにした時のことを思い出すと、ほとんど同様に、dequeにfoldを搭載することが可能になります。*8

まとめ

それなりに自分の頭の中では整理されていたので、いい記事になるだろうなぁと思いながら書いたのに、結局微妙になってしまい、思考のアウトプットが苦手で困るなぁという気持ちになっています。ご指摘あればお待ちしてます。ご精読ありがとうございました。

*1:そもそもブログの入りの挨拶から痛すぎてみてられない

*2:結合則を満たす演算を備えた集合のこと。よくわからなければ、整数での掛け算とかminとかgcdとか思っていただければ。

*3:知らないでもまあいい

*4:可換半群とは限らないので先頭要素から順番に積を考える

*5:多分stackは普通償却計算量じゃないかな…？最低でもstd::stackは実態がstd::dequeだったはずなので、償却のはず

*6:よくわからない人は可換の場合だけ考えるなら、とりあえず無視してok

*7:無駄をさらに削ぎ落としたものが、前回の記事のものなんですが、SWAGの概念をまず知るためには分かりづらい気がするんですよね。

*8:多分!!実装はしてません。もし実装するなら、生データはランダムアクセス可能なdequeとかを使って保持しておくと実装が楽かなぁという気がしてます。

2021-05-12

競プロ典型 90 問 037 - Don't Leave the Spice 解説

競技プログラミング

なんか面白い解法を見つけたので共有します。真に計算量が良い別の解法がある*1ので、そういうのを期待している人はブラウザバックです。

問題概要

【37 日目】
昨日の解説と今日の典型問題です。標準的な難易度となっています。なお、AtCoder ジャッジには 15 時頃に追加される予定です。（入力形式・入出力例は GitHub を参照のこと） #競プロ典型90問 pic.twitter.com/UpvDJT8Efy
— E869120@公開アカウント (@e869120) 2021年5月10日

問題文(AtCoder)
が十分簡潔なので, こちらを読みましょう。

考察

各調味料の量は、 $[L_i, R_i]$ の任意の実数を取りうるが、 $L_i, R_i$ 以外の量(以下中途半端な量と言う)となる調味料は高々1つとして良いことが証明できる。これは、もし最適な取り方に中途半端な量の調味料が2つあれば、片方を減らし、片方を増やすことで、どちらかを $L_i, R_i$ のいずれかに寄せることができるため、これを繰り返すことで、高々1つとして良いことが証明できる。
よって、中途半端な量となる調味料を固定することで、ナップサックDPの要領で、 $i$ 番目以外の調味料を使って、合計の量が $w$ のときの最大価値を求めることができる。例えば $N$ 番目を中途半端な量とすると

$\mathrm{DP}_{i,w} = (i$ 番目までの調味料で, 合計量 $w$ とした時の, 価値の最大値)

とすればDP可能である。ただし、これは1回のDPに $O(NW)$ かかり、 $N$ 回DPを行うため、 $O(N^2W)$ であり、定数倍改善の鬼でも通すのは困難である。*2

ここで、この複数回行うDPはかなり無駄があることに注目する。例えば、中途半端な量となる調味料が $N$ 番目の時と、 $N-1$ 番目の時は、ほとんど計算が一致している。さらに、DPする順番は入れ替えても問題がないことにも注意する。ここで

$\mathrm{DP}_{l,r,w} =$ ( $[l,r)$ 以外番目の調味料で, 合計量を $w$ とした時の, 価値の最大値)

と定める。すると、 $l\lt m\lt r$ に対して、 $\mathrm{DP}_{l,r,*}$ から $\mathrm{DP}_{l,m,*}$ 及び $\mathrm{DP}_{m,r,*}$ を $O( (r-l)W)$ で求めることができる*3。最終的に求めたいのは $0\leq i\lt N$ に対して $\mathrm{DP}_{i,i+1,*}$ を求めたい*4が、 $[0,n)$ -> $[0,n/2), [n/2,n)$ などのように順番に求めていけば、 $O(NW\log N)$ で求めたいものが求められる。

実装

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

inline bool chmax(ll&x,ll y)
{
    if(x<y){
        x=y;
        return true;
    }
    return false;
}

int main()
{
    int W, N;
    cin >> W >> N;
    vector<int> L(N), R(N);
    vector<ll> V(N);
    for(int i{}; i < N; ++i)
        cin >> L[i] >> R[i] >> V[i];
    auto op = [&](vector<ll> &v, int i){
        for(int j{W}; j >= L[i]; --j){
            chmax(v[j], v[j - L[i]] + V[i]);
            if(j >= R[i])
                chmax(v[j], v[j - R[i]] + V[i]);
        }
    };
    struct q{
        int l, r;
        vector<ll> v;
    };
    stack<q> st;
    {
        vector<ll> v(W + 1, LLONG_MIN);
        v[0] = 0;
        st.push(q{0, N, v});
    }
    ll ans{};
    while(!st.empty()){
        auto [l, r, v] = st.top();
        st.pop();
        if(r == l+1){
            for(int i{W-R[l]}; i <= W-L[l]; ++i)
                chmax(ans, v[i] + V[l]);
            continue;
        }
        int m = (l+r) / 2;
        auto vl = v, vr = v;
        for(int i{l}; i < m; ++i) op(vr, i);
        for(int i{m}; i < r; ++i) op(vl, i);
        st.push(q{l, m, vl});
        st.push(q{m, r, vr});
    }
    cout << (ans ? ans : -1) << endl;
}

提出 *5

まとめ

これ、有名テクだったりする？？？俺は知らない。最初平方分割しようとしたんだけど、平方分割できるときは結構セグ木ライクにできることが多いので、試しに考えたら生えた。最初価値がグラム単価だと誤読して生えた(ほぼ同様に解ける)んですが、 $O(NW)$ 解でもちょっと変形してやれば簡単に解けちゃうんですよね。*6価値が凸関数で与えられるとき*7とかは、この問題じゃないと解けないかな〜〜〜。*8実装がそこそこ綺麗にかけたので満足です。

追記

あれ？

dp1[i][j]:[0,i)で重みjの価値の最大値
dp2[i][j]:[i,n)で重みjの価値の最大値
（ただし使う重みはL,Rだけ）

として、i番目のだけ[L,R]で使うやつは
max_j ( dp1[i][j] + max_{k:[w-j-R,r-j-L]} dp2[i+1][k] )
で、これはjを全部見ながらkはdp2に対する幅R-Lのスライド最大値で出来ないかしら
— drogskol (@cureskol) 2021年5月12日

実は左右から累積するだけで $O(NW)$ で解ける。左右からやるとマージする必要があるから $O(NW^2)$ かかってしまうと思っていたんですが、最後に律儀にマージしなくても答えが導けるので、そんなことはないんですね〜。賢くてびっくりしてしまった。まあこの記事は元々計算量が良い記事というよりは、考え方が面白いよねーってだけなので、まあ別にいいんですが。

*1:具体的には自分の解法は $\Theta(NW\log N)$ で、 $\Theta(NW)$ の解法が存在します

*2: $O(NW^2)$ よりは希望がありそう

*3:普通にDPして伸ばせば良い

*4:いつの間にか0-indexに

*5:コンテスト中は私しか見れない

*6:公式解説のセグ木パートをスライド最大値に変更したものが、 $O(NW)$ 解ですが、スライド最大値に自分の価値-自分の重み*単価みたいのを突っ込んでやれば、同様に解けます。

*7:元問題は定数、誤読版は1次関数なのでともに凸関数

*8:凸であることは最初の中途半端な量が高々1つってところで使います。ところで

2021-04-24

ABC199 解説

競技プログラミングコンテスト解説記事

AtCoder Beginner Contest 199（Sponsored by Panasonic）の解説記事です。私は2100点(75:34)106位でした。

コンテストページ

A - Square Inequality

思考

オーバーフローなどが起きない制約であることだけ気をつけると、やるだけです。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    int a,b,c;
    cin>>a>>b>>c;
    puts(a*a+b*b<c*c?"Yes":"No");
}

コンテスト中のACコード

B - Intersection

思考

$A\leq x \leq B$ は $A\leq x$ かつ $x\leq B$ であることと同値です。

また $A\leq x$ かつ $A'\leq x$ は $max(A,A')\leq x$ と同値です。

同様に考えると、

「任意の $i$ について $A_i\leq x\leq B_i$ 」
$\Leftrightarrow$ 「任意の $i$ について $A_i\leq x$ かつ $x\leq B_i$ 」
$\Leftrightarrow$ 「 $\max\{A_i\}\leq x$ かつ $x\leq \min\{B_i\}$ 」
$\Leftrightarrow$ 「 $\max\{A_i\}\leq x\leq \min\{B_i\}$ 」

となるので、 $\max\{A_i\}, \min\{B_i\}$ の大小にだけ気をつければ良い。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;
    cin>>n;
    vector<int> a(n),b(n);
    int A=INT_MIN, B=INT_MAX;
    for(auto&i:a) cin>>i,chmax(A,i);
    for(auto&i:b) cin>>i,chmin(B,i);
    if(A>B) cout<<0<<'\n';
    else cout<<B-A+1<<'\n';
}

コンテスト中のACコード

C - IPFL

思考

クエリ2を愚直にやると1クエリに $\Theta(N)$ かかってしまい間に合いませんが、前半と後半を入れ替える操作は、前半と後半を別々に管理しておけば、今入れ替わっているかどうかだけ覚えておけば、クエリ1にもクエリ2にも対応することができます。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n,q;
    string s[2];
    cin>>n>>s[0]>>q;
    s[1]=s[0].substr(n);
    s[0]=s[0].substr(0,n);
    bool f=false;
    for(int i{},t,a,b;i<(q);++i){
        cin>>t>>a>>b;
        if(t==1){
            --a,--b;
            if(f) swap(s[1-a/n][a%n],s[1-b/n][b%n]);
            else swap(s[a/n][a%n],s[b/n][b%n]);
        }
        else{
            f=!f;
        }
    }
    if(f) cout<<s[1]<<s[0]<<'\n';
    else cout<<s[0]<<s[1]<<'\n';
}

コンテスト中のACコード

D - RGB Coloring 2

思考

塗り分けを全パターン考えると $3^N$ 通りあり、これは間に合いません。
隣あっている2つの頂点の色が別であるものだけ考えれば良いので、1つの頂点について色を決めたら、隣の頂点については2通りしか色を考えなくていいことがわかります。サイズ $S$ の連結成分について高々 $3\cdot2^{S-1}$ 通りだけ考えて、各連結成分についてのパターンの数をかけてやればいいことがわかります。

実装例

#include<bits/stdc++.h>
#include<atcoder/all>
using namespace std;
using namespace atcoder;
using ll=long long;

vector<vector<int>> e;
vector<int> c;
ll ans{1}, tmp;

void rec(vector<int>&g, int i=0){
    if(i==g.size()){
        ++tmp;
        return;
    }
    bool K[3]={};
    for(auto&j:e[g[i]]) if(j<g[i]){
        K[c[j]]=true;
    }
    for(int j{};j<(3);++j){
        if(!K[j]){
            c[g[i]]=j;
            rec(g,i+1);
        }
    }
}

int main(){
    int n, m;
    cin >> n >> m;
    e.resize(n);
    dsu d(n);
    c.assign(n,-1);
    for(int i{},a,b;i<(m);++i){
        cin>>a>>b;
        --a,--b;
        if(a>b) swap(a,b);
        e[a].push_back(b);
        e[b].push_back(a);
        d.merge(a,b);
    }
    for(auto g:d.groups()){
        sort(begin(g),end(g));
        tmp=0;
        rec(g);
        ans*=tmp;
    }
    cout<<ans<<'\n';
}

コンテスト中のACコード

E - Permutation

思考

各条件を考えるとき、重要なのは $a_1,a_2,\ldots,a_{X_i}$ の集合であって、順番は関係ありません。よって $S\subset\{1,2,\ldots,N\}$ に対して、

$\mathrm{dp}_S=$ (最初の $|S|$ 項の集合が $S$ である場合の数)

と定めると、 $X_i=|S|$ であるものについて、条件を満たしているか考えると、うまく遷移を作ることができ, $O( (N+M)2^N)$ *1とかで解くことができます。

実装例

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int main(){
    int n,m;
    cin >> n >> m;
    vector<ll> dp(1<<n);
    vector<vector<int>> Y(n), Z(n);
    for(int i{},x,y,z;i<(m);++i){
        cin>>x>>y>>z;
        Y[x].push_back(y);
        Z[x].push_back(z);
    }
    dp[0]=1;
    vector<int> p;
    for(int b{};b<(1<<n)-1;++b){
        p.assign(n+1,0);
        for(int i{};i<(n);++i){
            p[i+1]=p[i]+((b>>i)&1);
        }
        bool f=true;
        for(int j{};j<(Y[p[n]].size());++j){
            if(p[Y[p[n]][j]]>Z[p[n]][j]){
                f=false;
                break;
            }
        }
        if(!f) continue;
        for(int i{};i<(n);++i){
            if(((b>>i)&1)==0){
                dp[b|(1<<i)]+=dp[b];
            }
        }
    }
    cout<<dp[(1<<n)-1]<<'\n';
}

コンテスト中のACコード

F - Graph Smoothing

思考

$k$ 回の操作後に頂点 $1,2,\ldots,N$ に書かれている数の期待値( $E_i$ )がわかっている時, $k+1$ 回の操作後に頂点 $1,2,\ldots,N$ に書かれている数の期待値を考えます。
これは辺 $(X_i,Y_i)$ が選ばれた時、頂点 $X_i,Y_i$ はともに $\frac{E_i+E_j}2$ が期待値であり、それ以外の頂点 $l$ は、 $E_l$ が期待値となります。全ての辺が一様に選ばれることに注意すると、これから、 $k+1$ 回の操作後の期待値は、 $k$ 回の操作後の期待値を並べたベクトルに、行列をかけてやることで求まることがわかります。よって行列累乗によって、十分高速に求めることができます。

実装例

#include<bits/stdc++.h>
#include<atcoder/all>
using namespace std;
using namespace atcoder;

using mint = modint1000000007;

template<class T> struct mat;\\行列のライブラリ

int main(){
    int n,m,k;
    cin >> n >> m>> k;
    vector<vector<mint>> a(n,vector<mint>(1));
    int tmp;
    for(auto&i:a){
        cin>>tmp;
        i[0]=tmp;
    }
    mint iv=mint(m).inv(), iv2=iv/2;
    vector<vector<mint>> e(n,vector<mint>(n));
    for(int i{},x,y;i<(m);++i){
        cin>>x>>y;
        --x,--y;
        for(int i{};i<(n);++i){
            if(i!=x and i!=y){
                e[i][i]+=iv;
            }
        }
        e[x][x]+=iv2;
        e[x][y]+=iv2;
        e[y][x]+=iv2;
        e[y][y]+=iv2;
    }
    for(auto v:(mat<mint>(e).pow(k)*mat<mint>(a)).v){
        cout<<v[0].val()<<'\n';
    }
}

コンテスト中のACコード

終わりに

Panasonicさん、いつもお世話になっております(2回目)。

*1:もうちょっと早い

2021-03-27

ABC197 解説

競技プログラミングコンテスト解説記事

AtCoder Beginner Contest 197（Sponsored by Panasonic）の解説記事です。なんか暇だったので久々に解説記事を書いてみました。2100点(51:37)67位でした。

コンテストページ

A - Rotate

思考

最初長さ3に気づかず、for文要求してね？って思った。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    string s;
    cin>>s;
    cout<<s[1]<<s[2]<<s[0]<<'\n';
}

コンテスト中のACコード

B - Visibility

思考

自分のいるところから、#に当たるまで移動して数えれば良いです。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    int h,w,x,y;
    cin>>h>>w>>x>>y;--x,--y;
    vector<string> s(h);
    for(auto&c:s) cin>>c;
    int ans{1};
    for(int i{x-1};i>=0;--i){
        if(s[i][y]=='#') break;
        ++ans;
    }
    for(int i{x+1};i<h;++i){
        if(s[i][y]=='#') break;
        ++ans;
    }
    for(int j{y-1};j>=0;--j){
        if(s[x][j]=='#') break;
        ++ans;
    }
    for(int j{y+1};j<w;++j){
        if(s[x][j]=='#') break;
        ++ans;
    }
    cout<<ans<<'\n';
}

コンテスト中のACコード

C - ORXOR

思考

区間の分け方は, 仕切り(N-1)個を入れるかどうかの $2^{N-1}$ 通りなので, bit全探索で計算すれば間に合います。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    unsigned n;
    cin>>n;
    vector<unsigned> a(n);
    for(auto&i:a) cin>>i;
    unsigned ans{UINT32_MAX};
    for(int b{};b<(1<<(n-1));++b){
        unsigned x{}, tmp=a[0];
        for(int i{};i<(n-1);++i){
            if((b>>i)&1){
                x^=tmp;
                tmp=a[i+1];
            }
            else{
                tmp|=a[i+1];
            }
        }
        chmin(ans, x^tmp);
    }
    cout<<ans<<'\n';
}

コンテスト中のACコード

D - Opposite

思考

0番目の点とN/2番目の点の中点が中心になります。中心からみて $\frac{2\pi}N$ 回転させたところにあるので, 回転行列考えて

$\begin{align*} \begin{pmatrix} x_1 \\ y_1 \\ \end{pmatrix} = \begin{pmatrix} \cos\frac{2\pi}N & -\sin\frac{2\pi}N \\ \sin\frac{2\pi}N & \cos\frac{2\pi}N \\ \end{pmatrix} \left( \begin{pmatrix} x_0 \\ y_0 \\ \end{pmatrix} - \begin{pmatrix} \frac{x_0+x_{N/2}}2 \\ \frac{y_0+y_{N/2}}2 \\ \end{pmatrix} \right) + \begin{pmatrix} \frac{x_0+x_{N/2}}2 \\ \frac{y_0+y_{N/2}}2 \\ \end{pmatrix} \end{align*}$
を計算すれば良い。

実装例

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n;
    long double x,y,X,Y,cx,cy,r,pi=3.14159265*2;
    cin>>n>>x>>y>>X>>Y;
    cx=(x+X)/2;cy=(y+Y)/2;
    r=sqrt((x-cx)*(x-cx)+(y-cy)*(y-cy));
    cout<<setprecision(20)<<(cx+(x-cx)*cos(pi/n)-(y-cy)*sin(pi/n))<<" "
    <<(cy+(x-cx)*sin(pi/n)+(y-cy)*cos(pi/n))<<'\n';
}

コンテスト中のACコード

E - Traveler

思考

(なんで色にしたんだろう)
広義単調増加に回収していくので、Cの値ごとに座標をまとめて、小さい方から訪れることを考えます。同じ値を回収する順番ですが、まず一番右のを回収してから、一番左のを回収するか、その逆以外は考える必要がありません(無駄なので)。ですから、Cの値ごとに、C以下を全部回収するのにかかる時間を、最終位置が一番左の時と最終位置が一番右の時とで分けて管理しておけば良いです。
オーバーフローに気をつけよう(1敗)。

実装例*1

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int main(){
    int n;
    cin>>n;
    vector<vector<int>> v(n);
    for(int i{},x,c;i<(n);++i){
        cin>>x>>c;
        v[--c].push_back(x);
    }
    ll l{},cl{},r{},cr{};
    ll nl{},ncl{},nr{},ncr{};
    for(int i{};i<(n);++i){
        if(v[i].empty()) continue;
        sort(v[i].begin(),v[i].end());
        nl=v[i].front();
        nr=v[i].back();
        ncl=min(abs(l-nr)+nr-nl+cl, abs(r-nr)+nr-nl+cr);
        ncr=min(abs(l-nl)+nr-nl+cl, abs(r-nl)+nr-nl+cr);
        l=nl,r=nr,cl=ncl,cr=ncr;
    }
    cout<<min(cl+abs(l),cr+abs(r))<<'\n';
}

コンテスト中のACコード

F - Construct a Palindrome

思考

回文と言うのは、外側から攻めるか、中心から攻めるかだと思うのですが、計算量に余裕がありそうなので、中心全探索とかかなーと思って無駄な時間を過ごします。
外側から、同じ文字のときに1個ずつ進めるみたいなことをしたいなと思うと、まず(1,N)のペアから、1とNから生えている同じ文字の辺を辿って、みたいなことを連鎖的にやって、同じ頂点のペアor辺で繋がれた頂点のペアが現れれば、そこを中心とする回文になっています。よってpairをkeyとするBFSをすれば良いです(ただ奇数長と偶数長があるので、打ち切るタイミングに気をつけましょう)。

実装例*2

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n,m;
    cin>>n>>m;
    vector<vector<pair<int,char>>> e(n);
    bool v[1000][1000]={};
    for(int i{},a,b;i<(m);++i){
        char c;
        cin>>a>>b>>c;--a,--b;
        v[a][b]=v[b][a]=true;
        e[a].emplace_back(b,c);
        e[b].emplace_back(a,c);
    }
    using ti = tuple<int,int,int>;
    priority_queue<ti, vector<ti>, greater<>> pq;
    vector<vector<bool>> cc(n,vector<bool>(n,false));
    pq.emplace(0,0,n-1);
    int ans{INT_MAX};
    while(!pq.empty()){
        auto[c,i,I]=pq.top();pq.pop();
        if(ans<=2*c) break;
        if(i==I){
            chmin(ans, 2*c);
            break;
        }
        if(v[i][I]){
            chmin(ans,2*c+1);
            continue;
        }
        for(auto[j,cj]:e[i]) for(auto[J,cJ]:e[I]) if(cj==cJ){
            if(cc[j][J]) continue;
            cc[j][J]=true;
            pq.emplace(c+1, j, J);
        }
    }
    cout<<(ans==INT_MAX?-1:ans)<<'\n';
}

コンテスト中のACコード

終わりに

Panasonicさん、いつもお世話になっております。

*1:各値の最大値と最小値を管理するだけでいいんですが、めんどいのでソートをしているので、計算量に $\log$ が乗っています。

*2:勢いでDijkstraを書いてしまっていますが、BFSの方が計算量は良いです。Dijkstraでも余裕で間に合いそうなので、途中で気付きましたがそのまま書いちゃいました。

2021-01-03

2021年の目標

2020年の振り返り

大体AtCoder橙になりました - Motsu_xe 競プロのhogeやfugaを読めばいいと思います。

一応これ以降の出来事ですが、ARC110(鹿島建設プロコン)がNoSub、AGC050(Goodbye rng_58 Day1)で+24、AGC051(Goodbye rng_58 Day2)で+43とかで、現在レート2476となっております。

2020年は、2091->2476(+385)で大体1色上がった感じで、とある情報筋によると日本で39番目くらいにのびたらしいです。実力的には出来過ぎなくらいかなぁと思ってしまいますが。。。

2021年の抱負

最低限2600になる。
できれば2700になる。
ICPCで国内予選突破する。

真面目に書こうかとも思ったがめんどくなったのでここらへんで筆をおくことにします。

2020-12-07

AtCoder橙になりました

この記事は「色変記事 Advent Calendar 2020」7日目の記事です。

事の始まり

色変記事AdventCalendarを作成しました。
みなさまの勇気ある宣言をお待ちしております！https://t.co/1NqMxq7Wu3
— どきん@youtubeはじめました (@ayoiyouyoeyo) 2020年11月4日

TLに流れてきた狂気のアドベントカレンダー。そして、そのときの私のレート
f:id:Motsu_xe:20201206220525p:plain

橙になるまで残り+75。今年の目標として橙になることを上げていた私は、このアドカレに登録するかどうか、悩む。悩む、悩み、悩んだが、ついに登録しようと決心。しかし、その時点でアドカレの後半は既に埋まっており、AGC1回, ARC3回で橙にならねばならないことが確定。そして

登録した、色変してやるぞ https://t.co/NFcSiDUywd
— Motsu_xe (@Motsu_xe) 2020年11月4日

結果

苦節云年、ついに、橙コーダーになりました！！！！！うおおおおおおおおおお pic.twitter.com/5TxFyH03ws
— Motsu_xe (@Motsu_xe) 2020年11月28日

というわけで、ARC109にて、ついに橙コーダーになることと相成りました！最高！！！

橙コーダーになるまでにしたこと

以前
motsu-xe.hatenablog.com
こういう記事を書いた*1ので、主に2020年に何をやったかを話したいと思います。

とりあえず各種データを持ってきます。
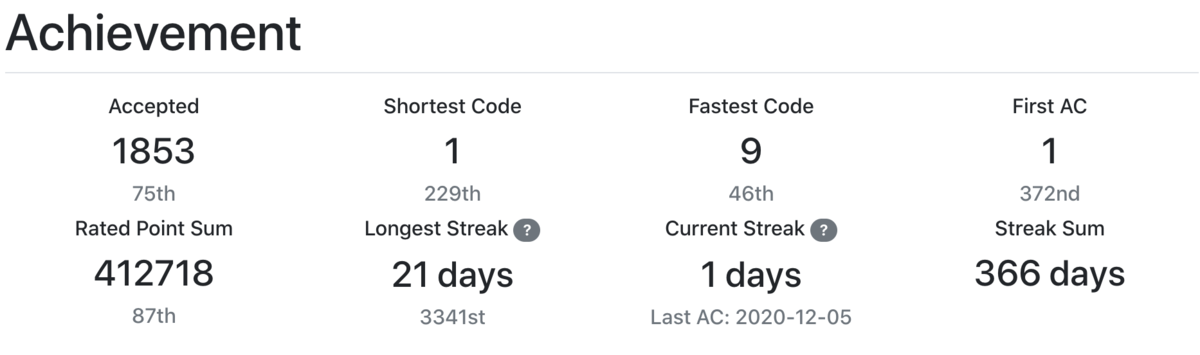
f:id:Motsu_xe:20201206222344p:plain
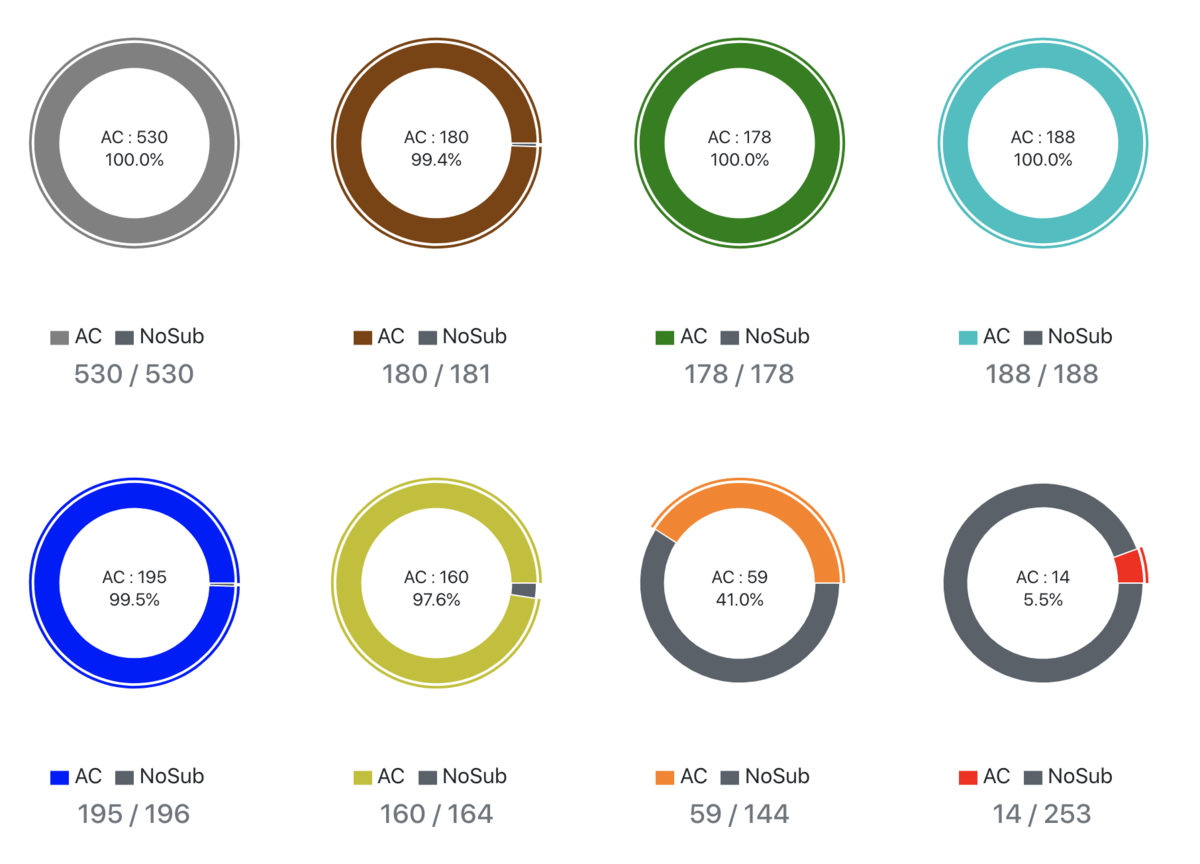
f:id:Motsu_xe:20201206222400p:plain
f:id:Motsu_xe:20201206222415p:plain
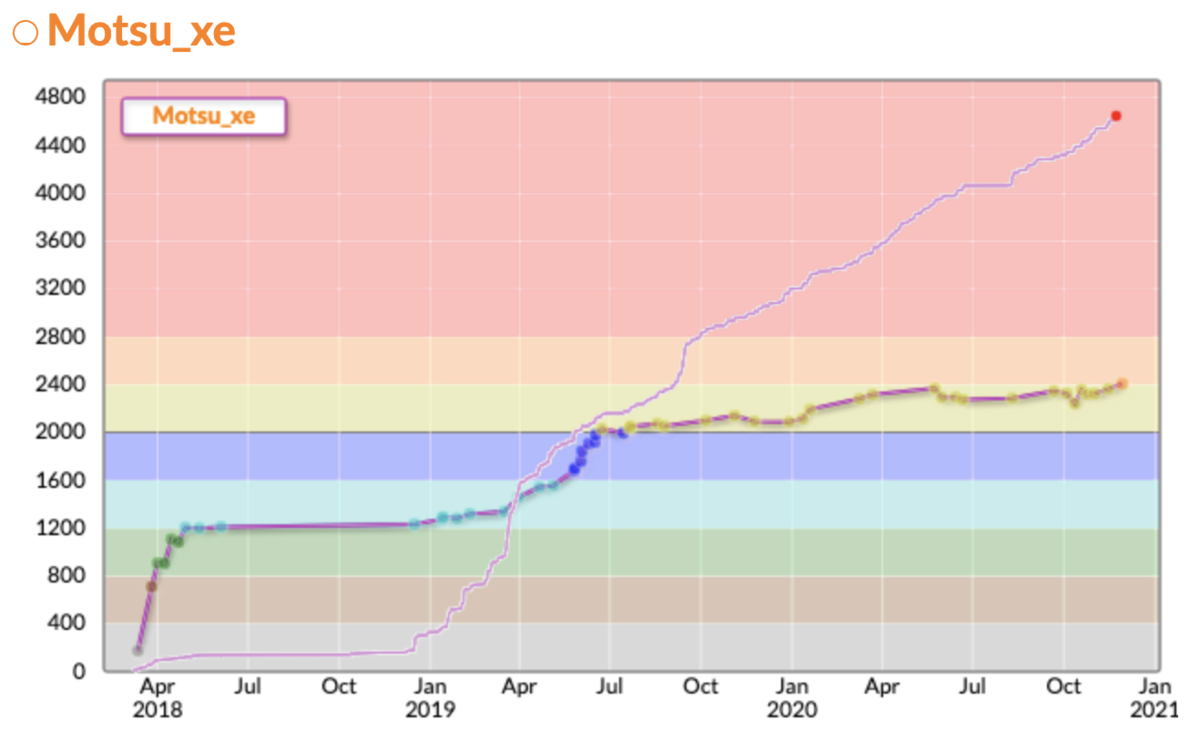
f:id:Motsu_xe:20201206222429p:plain

えーー、ご覧になるとお分かりになると思いますが、2020年、全然競プロをやっておりません。精進グラフはコンテストに出れば勝手に増えていくので、要はまあいわゆる精進はしていませんね。

これはAtCoderに限った話なのですが、Codeforcesも薄橙にならないと使えない機能があるとか小耳に挟んだ*2ので、薄橙になるために何回か出ただけでまともにやっていません。

またICPCの予選に出場*3したので、そのための精進はしていたんですが、構文解析担当だったので、そればっかやっており、AtCoder力には大きな影響はなかったと思います。

では何故レートが上がったのか。これはコンテストが上手くなったという話に集約されると思います*4。

コンテストの技術

競技プログラミングは"競技"ですから、実力を測るものではなく、コンテストで競って勝つことがレートを上げる唯一の方法です*5。

「
彼を知り己を知れば百戦殆からず」という言葉があります*6。意味はよく知りませんが、敵と自分をの状況を完全に把握さえできれば最強であるというような意味でしょうおそらく。ここで彼とは自分以外の参加者であり、己とは自分のことです。

競プロでレートを上げたいのであれば、コンテストで高順位*7をとる必要があります。ですから、他の参加者がどのくらい問題を解けて、自分がそれに勝ちうるような選択をする必要があります。

彼を知る

私は彼をよく知らないので、何とも言えませんね。今後の課題かも。

例えばですが、AtCoderユーザーは割と前から順番に解いていくのが好みなようで、順位表のABCとABCDの間とかには人が結構少ないことがわかります。なので、例え3完しかできなくても、ABDとかを解いていれば、まあギリギリ4完した人と同じくらいのPerf.を出せるわけです。Wow。

己を知る

ところで私の2020年3月以降、レートを+10以上した回の正答状況をみてみましょう。

ARC109	ABCE
AGC049	BCD
AGC048	ACD
ACLC1	ABCE
AGC047	ABE
AGC044	AC
AGC043	AD
日立PC	ABCE

というように、まあ前からちゃんと解いてみたいな方法をしている回はただの1度もありません(逆にいうならそうしている回はレート変動は+9以下であるということです)。

またこのような情報もあります。

あなたのレートはどこから？
私は
AGC: 196
ARC: -136
ABC: 0
Other: -13
(直近6ヶ月)

あまりにも露骨で、涙＿＿＿
ほんまにARC出るべきじゃないな

https://t.co/axVYYOZZQX
— Motsu_xe (@Motsu_xe) 2020年11月15日

ここからわかるのは、とりあえず問題飛ばして高難度を強引に通すというような解き方でしかレートを上げられないし、そもそもARCではレートが上がらないし、AGCでは大体上がるということもわかります。

こうなっている原因の考察も重要ですが、この傾向でどう戦略を組み立てるかも重要です。まず一番露骨な戦略では

もう自分はARCは毎回潜伏して、高難易度mod998(or 1e9+7)を解く戦略が最適な気がするな
— Motsu_xe (@Motsu_xe) 2020年11月28日

というものがあります。*8この戦略は近3回で実施しましたが、1勝2NoSubです。mod問題はサンプルが強いがちなので、NoSub戦略最大のデメリットであるところの、あってると思って提出したら通らなくて破滅が発生し辛いというものがあります。

他にも、AGCに置いても低難度を破壊した後は、後半の問題を眺めるとかの戦略が良いとわかります。

全人類これでいいじゃないかと思われるかも知れませんが、そんなことはなくて、高難度問題で得意問題を判別する能力が必要です。私は得意不得意がかなり露骨なので、何となくみたら解けそうか解けなそうかが見える*9のでこの戦略がはまっているだけで、満遍なく得意な人とかは、素直に前から解いていくのが良いケースが多いとは思います。

終わりに*10

競技プログラミングは毎回敵との斬り合い、楽しいね！一番いいのは高レートの人がA問題を通したところで闇討ちするのが最適戦略なんですが、うまいこと行きませんね。念を送ったりはしているのですが。何の記事だったんだろこれ。

おまけ

色変に失敗したときに作ろうと思ってたもののラフ
f:id:Motsu_xe:20201206230911g:plain

*1:今さらタイトルの誤字に気づいたが、放置＿＿＿_

*2:結局これが何なのかわからない

*3:惜しくも敗退

*4:当然全く問題を解いていないわけでもないので、実力も上がってはいるはずではありますが

*5:たまに精進しても何でレートが上がらないのかという人がいますが、これは自明でコンテストで勝利していないからです。

*6:孫子ね。同感だわ

*7:高得点ではない。3完最速と4完最遅の価値は大体同じ

*8:南米の主婦層の辺りにはNoSubは犯罪だと言っている族もいるが、とんでもないNoSubは合法なんだよ。

*9:当然外して破滅することもある

*10:大体記事というものは書き始めたときは意気揚々としてるけど、途中で文才の無さに絶望してだれてくるのがよくないわね。

2020-10-13

オフライン・オンライン変換

競技プログラミングアルゴリズム

本記事ではオンライン・オフライン変換と呼ばれる動的計画法(DP)の高速化テクニックの1つを解説していこうと思います。お気持ち理解重視で書くので、冗長かもしれませんがお付き合いください。

高速化テクニックと言いましたが、これ自体は高速化テクニックではなく、「オンラインDP」と呼ばれる種類のDPを、「オフラインDP」と呼ばれる種類のDPに帰着させるテクニックです。一般に前者より後者の方が扱いやすく、結果的に高速化できる場合があるという話になります。

オンラインDPとは

まずオンラインDPとは何か説明していきます。厳密に定義付けられた言葉なのか知りませんが、簡単に言えば「DPテーブルの計算にDPテーブルを用いるDP」ということができます。例えば一般的な2項間漸化式のようなDP

$\begin{align*} \mathrm{DP} _ i=\mathrm{DP} _ {i-1}^3+2 \end{align*}$

のようなものはオンラインDPです。またLCSを求めるDP

$\begin{align*} \mathrm{DP} _ {i,j}=\max(\mathrm{DP} _ {i-1,j},\,\mathrm{DP} _ {i,j-1},\,\mathrm{DP} _ {i-1,j-1}+\mathrm{is\_equal} (s_i,\,t_j)) \end{align*}$

などもオンラインDPです。

オンラインDPの特徴は、一般項などを見つけない限りは、DPテーブルを順番にしたがって埋めていかなければならないということです。この制限は強く、高速化することが難しくなってしまいます。

オフラインDPとは

次にオフラインDPとは何かを説明していきます。簡単に言えば、オンラインDPでないDP、すなわち「DPテーブルの計算にDPテーブルを用いないDP」です。例えば以下のような問題はオフラインDPの一種です。

$\begin{align*} \mathrm{DP} _ j=\max\{|i^2-j|;\,i\in[0,j)\} \end{align*}$

これを見て、これはDPなのか？ただ関数を計算しているだけではないのか？と思うかもしれませんが、極論突き詰めるとオフラインDPとはこういうものです。こんな問題は出ないと思うかもしれませんが、例えば典型的な0-1ナップザック問題を $O(NW)$ で解くDPの遷移は

$\begin{align*} \mathrm{DP} _ {i,j}=\max(\mathrm{DP} _ {i-1,j},\,\mathrm{DP} _ {i-1,j-w_i}+v_i) \end{align*}$

ですが、これは実は(部分的に)オフラインDPになっています。つまり $\mathrm{DP} _ {i}$ なるテーブルを埋めるのに、 $\mathrm{DP} _ {i-1}$ しか使っていないため、すでに $\mathrm{DP} _ {i-1}$ を埋めている状況に於いて、これはオフラインDPと言えます。

オフラインDPの特徴は、テーブルを埋める順序を気にせずに計算して良いということです。これにより、都合よい順番で埋めていくことによって、高速化できることがあります。

お気持ち

ナップザックの2次元DPなどは、DPテーブルに依存していると言えば依存しているので、あくまで部分的にオフラインという話なので、オンラインと言えばオンラインと言えます。つまりこれはオフラインDPを繰り返し適用しているということになります。

これは極論を言えば、任意のオンラインDPも1項だけ埋めるオフラインDPを繰り返してると解釈することもできて、じゃあ何が違うねんみたいな気持ちになるかもしれません。なのでちょっとDPを一般論っぽく話をしてみたいと思います。

DPの添字集合を $I$ (有限集合)、DPのとる値の集合を $V$ として、各 $i\in I$ に対して $\Lambda_i\subset I$ と $F_i:V ^ {\Lambda_i}\to V$ が定まっているとする*1。このとき $I$ 上の半順序が $i\lt j \Leftrightarrow i\in\Lambda_j$ で定まるとする(この順序による有向グラフが閉路を持たなければ良い)。このとき、半順序にしたがった順番で

$\begin{align*} \mathrm{DP} _ {i}=F_i( (\mathrm{DP} _ j;\,j\in\Lambda_i) ) \end{align*}$

を計算することをDPと呼ぶことにする( $i$ が極小元(つまり $\Lambda _ i=\emptyset$ )のときは、 $F_i$ が一点集合からの定値関数となってます)。

このときオンラインDPとは、半順序のトポロジカルソートの自由度が低い(一意乃至ほぼ一意)DP、オフラインDPはその自由度が高いDPと言い換えることができる。

オンライン・オフライン変換

オンライン・オフライン変換というのは、一部のオンラインDPをオフラインDPに変換して計算の自由度を上げようという試みです。オフラインに変換できるならそれは元々自由度が高いじゃないかみたいな気持ちになると思うのですが、まあこれは特殊なDPにしか適用できません(とはいえ、一般的なDPには大体適用できますが)ので、許してください。

条件を整理する前に、前項で定義した語を、簡単のために言い換えておくことにします。以後 $I$ はトポロジカルソートされている*2ものとします。また分かりづらいので、 $I=[0,N)$ として*3、 $\Lambda_i=[0,i)$ とします*4。

条件というのは、 $V$ がモノイドで、任意の $i\in [0,N),\,j\in[0,i)$ について、 $F _ {i,j}:V\to V$ が存在して $F _ i(v _ 0,v _ 1,..,v _ {i-1})=F _ {i,0}(v _ 0) F _ {i,1}(v _ 1) .. F _ {i,i-1}(v _ {i-1})$ (モノイドとしての積)となることです。*5

仰々しく書いていますが、要は参照するDPテーブルを途中で切って、それぞれについて計算した後マージすることができれば良いということです。つまりよく出てくるような $j$ についてなんやかんや計算して、足したり $\max,\min$ を取ったりするものに関してはOKということです*6。

オンラインDPも細かく区切ればオフラインDPという話をしましたが、答えをマージできるがために、うまい具合に区切って、小さなオフラインDPの集まりと考えることができるようになるということです。

では具体的な方法を与えます。 $\mathrm{DP} _ {i,l,m}$ を

$\begin{align*} \mathrm{DP} _ {i,l,m}=\prod _ {j=l} ^ {m-1} F _ {i,j}(\mathrm{DP} _ j) \end{align*}$

と定義します。このとき $\mathrm{solve} (l,\,r)$ を $i\in[l,\,r)$ に対して $\mathrm{DP} _ {i,l,i}$ を計算する関数、 $\mathrm{induce} (l,\,m,\,r)$ を $i\in[m,\,r)$ に対して $\mathrm{DP} _ {i,l,m}$ とします。求めたいのは $\mathrm{DP} _ i=\mathrm{DP} _ {i,0,i}$ に気をつけて、 $\mathrm{solve} (0,\,N)$ となります。

ここで次のような疑似コードで $\mathrm{solve} (0,\,N)$ を呼ぶことを考えます(ただし $e$ は $V$ の単位元)。

dp = [e] * N

induce(l, m, r):
     #hoge

solve(l, r):
    if l + 1 == r:
        return
    m = (l + r) // 2
    solve(l, m)
    A = induce(l, m, r)
    for i in [m, r):
        dp[i] *= A[i]
    solve(m, r)
    return

これが正しく回っていることの確認は各自に任せます*7。

今 $\mathrm{induce} (l,\,m,\,r)$ がオフラインDPとなっています。これは $\mathrm{induce} (l,\,m,\,r)$ が呼ばれる時点で $i\in[l,m)$ に対して $\mathrm{DP} _ i$ がすでに求まっており、 $\mathrm{DP} _ {i,l,m}$ はそれにのみ依存しているためです。よって $\mathrm{induce} (l,\,m,\,r)$ を求める際は、律儀に $m,m+1,..,r-1$ の順番で求めずとも、適当な順番で求めても良いということになります。

以上でいくつかのオフラインDPに分解することができました。ここで計算量を考える。 $N=r-l$ として、 $\mathrm{solve} (l,\,m,\,r)$ の計算量を $T(N)$ , $\mathrm{induce} (l,\,m,\,r)$ の計算量を $M(N)$ とすると

$\begin{align*} T(N)=2T(N/2)+M(N) \end{align*}$

となり、 $T(N)=O(M(N)\log N)$ となります。*8

一つ気を付けたいのは、オンラインDPをなんでもかんでもオフライン化しても、 $M(N)$ が抑えられない限り高速化はされないということです。

具体例

これだけ見てもよくわからないかもしれないので、簡単な問題を解いてみます*9。

整数 $N\leq 10 ^ 6$ と長さ $N$ の整数列 $X$ について、 $\mathrm{DP} _ 0=0$ として、

$\begin{align*} \mathrm{DP} _ {i}=\min\{|\mathrm{DP}[j]-X[i]|; \, j \in [0,i)\} \end{align*}$

により計算される配列を求めよ。

という問題を考えます。愚直にやると $O(N ^ 2)$ かかり間に合いませんが、前からsetに $\mathrm{DP}[i$ ]を突っ込んでいって、set上の二分探索とかで $X[i$ ]に一番近いやつを求めてやれば $O(N\log N)$ で十分高速に求めることができます。

…で終わりだとなんの記事だよって話なんですがこれはオフライン・オンライン変換でも求めることができます。

まずオフラインへの変換は問題によらず変わらないので、 $\mathrm{induce} (l,\,m,\,r)$ を考えます。 $\mathrm{dp}[l,m)$ をソートして、 $i\in [m,r)$ について、ソートした数列上を $X_i$ で二分探索すれば、簡単に求めることができます。これのオーダーは $O(N\log N)$ なので、全体で $O(N\log ^ 2 N)$ で解くことが出来、十分高速です。

C++で実装したものが以下となります。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
void chmin(ll&x,ll y){
    if(x>y) x=y;
}

int N;
vector<int> X;
vector<ll> dp;

void induce(size_t l, size_t m, size_t r){
    vector<ll> tmp(m - l);
    copy(dp.begin() + l, dp.begin() + m, tmp.begin());
    sort(tmp.begin(), tmp.end());
    for(size_t i{m}; i != r; ++i){
        size_t j = lower_bound(tmp.begin(), tmp.end(), X[i]) - tmp.begin();
        if(j > 0) chmin(dp[i], abs(tmp[j - 1] - X[i]));
        if(j < m - l) chmin(dp[i], abs(tmp[j] - X[i]));
    }
}

void solve(size_t l, size_t r){
    if(l + 1 == r)
        return;
    size_t m = (l + r) / 2;
    solve(l, m);
    induce(l, m, r);
    solve(m, r);
}

int main(){
    cin >> N;
    X.resize(N);
    for(auto &i : X) cin>>i;
    dp.assign(N,LLONG_MAX);
    dp[0] = 0;
    solve(0,N);
    for(auto &i : dp) cout << i << " ";
    cout << endl;
}

またこのままでも十分高速ですが、 $\mathrm{dp}[l,m)$ をマージソートっぽくソートして、 $X$ も予めマージソートした途中経過を全部覚えておくと、二分探索パートを尺取法っぽくすることで、 $\mathrm{induce} (l,\,m,\,r)$ の計算量を $O(N)$ に抑えられて、全体で $O(N\log N)$ に抑えることができ、setに劣っていないことが分かりますね！*10

まとめ

以上長くなりましたがオフライン・オンライン変換のお話でした。本質パートはかなり単純なんですが、使い所がややこしい影響で、理解しにくいような気がしたので、本質だけ切り抜いて説明しようとしたんですが、なんかごちゃごちゃしすぎて逆に分かりづらいかもしれません。

再掲すると「答えをマージできるがために、うまい具合に区切って、小さなオフラインDPの集まりと考えることができるようになるということです。」←これが本質だと思っています。

なんかわからなかったらTwitterでもコメントでもいいので書いてくれると助かります。以上、ご精読ありがとうございました。

参考文献

動的計画法高速化テクニック（オフライン・オンライン変換） - Qiita

大体これで学んだし、半分以上これのパクリですすいません。

*1:この $F _ i$ は $j\in\Lambda _ i$ を用いて記述されることが多いが、それは $F_i$ が複数乃至全ての $i$ について同時に定義されるがためにそうなっているだけで、単一の $i$ については、そのような $j$ は定数となるから $\mathrm{DP}_j$ のみの関数として与えられることに注意してください

*2:オンラインなら一意なソートと考えていいです

*3:ソート済の有限集合なのでこうして良い

*4: $\Lambda_i\subset {1,\,..\,i-1}$ であり、定義域を広げる分には、広げた分だけ無視すればいいのでOKです

*5:まあ実際はもうちょい弱くてもでき~~ますが、こんなもんでしょう~~て、 $a _ i,b _ i\in V$ を用いて $F _ i(v _ 0,v _ 1,..,v _ {i-1})=a _ iF _ {i,0}(v _ 0) F _ {i,1}(v _ 1) .. F _ {i,i-1}(v _ {i-1})b _ i$ くらいはOKです。まあつまり初期化をいじったり、最後に追加で作用する分にはいいということです。こうしとか無いと初期値が単位元で固定されてよく無いですね(後述の具体例では $i=0$ でだけ初期値をいじってます)。

*6:分かりづらければ、下の具体例の問題を想像していてください

*7:solve(l,r)が呼ばれる時点で、 $i\in[l,r)$ に対して $\mathrm{dp}[i$ =\mathrm{DP} _ {i,0,l}]となっていることなどを、帰納法の中で帰納法回したりすれば示せます。もっと簡単な方法もあるかも

*8:コメントで議論があったので、注釈を入れておきます。まず $M(N)=\Omega(N)$ を仮定しています。これはどちらにせよinduceの後に今までの結果とmergeするパートがあるので、それを合わせれば $\Omega(N)$ にはなるからです。ただ更新する必要がある場所が疎な場合(またその場合に限り) $M(N)=o(N)$ となる場合もありますが、その場合でも $T(N)=\Omega(N)$ にはなりますので注意してください。また例えば $M(N)=O(N ^ 2)$ の場合は、二乗の木DPと同じ計算量で $T(N)=O(N ^ 2)$ となりますが $O(N ^ 2)=O(N ^ 2\log N)$ なので、先の評価でちゃんと上から抑えることはできてます(ところでオーダー表記の等号が非可換なのどうにかならんかね)。

*9:大体オンライン・オフライン変換はMonotone-Minimaがセットでそっちが難しいから難しく感じてしまう気がする

*10:実装はめんどいのでしません()